Harmooniline rütm

Seto leelo muusikalise stiili üks tähtsamaid ja omapärasemaid ilminguid on harmooniline rütm (edaspidi kasutan ka lühendit HR) (vt Pärtlas 2001, 2006a, 2021). See on seto leelo alusprintsiip, mis määrab mitmehäälse faktuuri ülesehituse, kooskõlade intervallistruktuuri ja individuaalsete häälte meloodilise varieerimise. Ühtlasi on HR viisitüübi peamine representatiivne tunnus, kuna see eristab viise üksteisest ja jääb stabiilseks ka viisi varieerimisel. Harmooniliseks rütmiks nimetan kahe harmoonilise astmekompleksi (harmooniafunktsiooni) vaheldumise rütmi. Binaarne harmoonia on tuntud paljudel Euroopa rahvastel, eriti (uuemas) pillimuusikas (vt Morgenstern 2022), kuid seto leelo puhul on tegemist haruldasema nähtusega – arhailise modaalse harmoonilise süsteemiga, kus binaarne harmoonia avaldub vokaalses mitmehäälsuses.

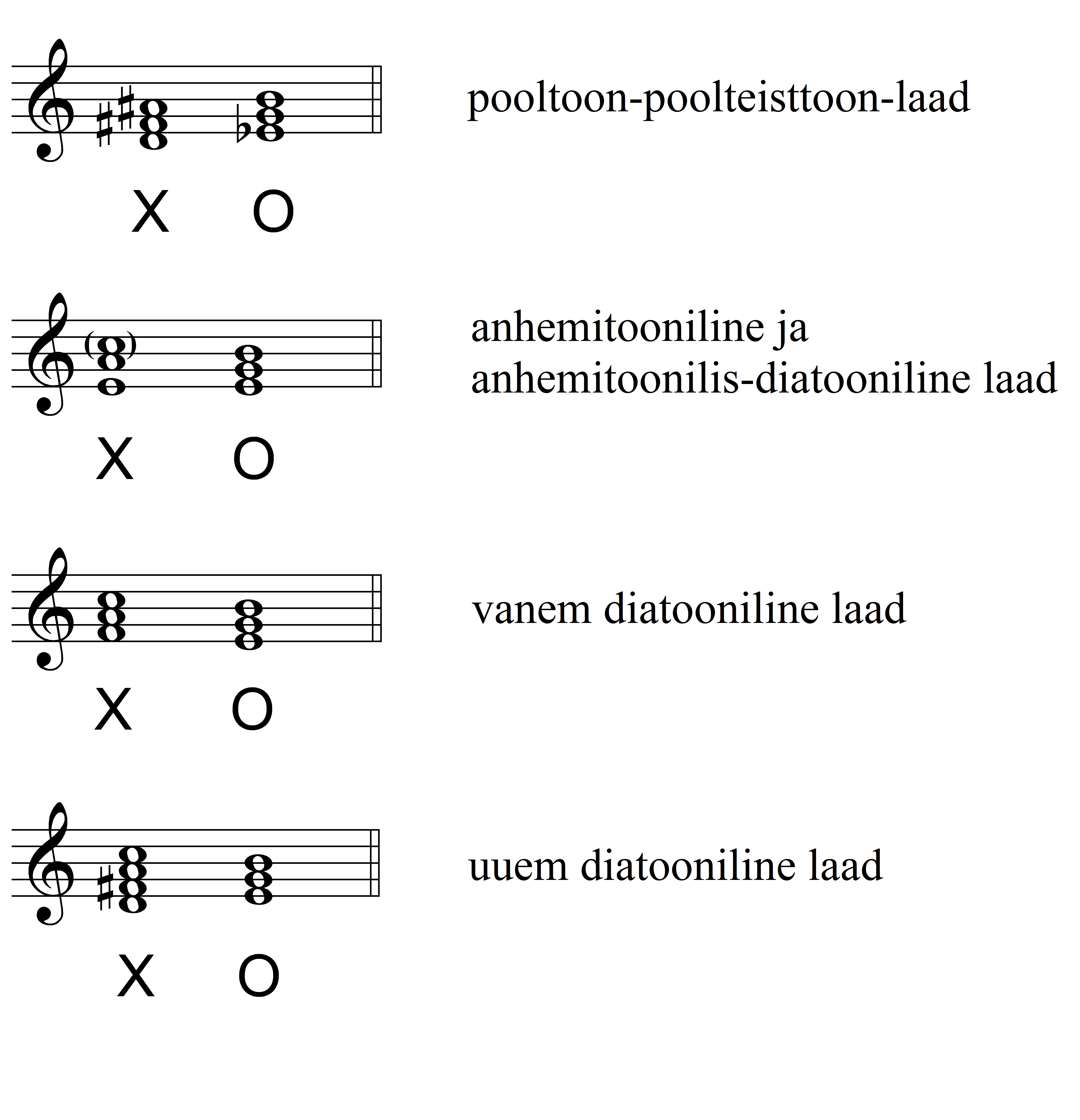
Peatükis Helilaadid on lähemalt selgitatud seto eri heliridade astmete jagunemist kaheks funktsionaalseks kompleksiks nn „ülehüppamise“ printsiibil (Überspringverfahren Gerhard Kubiku järgi (1968)). See tähendab, et ühte kompleksi kuuluvad helireas üle ühe asetsevad astmed. Komplekside intervalliline struktuur sõltub konkreetse helirea struktuurist. Helilaadide peatükis on iga helirea puhul näidatud, millised harmoonilised kompleksid vastava helirea astmetest moodustuvad. Meeldetuletuseks on need esitatud ka siin (vt näidet 1). Eri helilaadide astmekomplekse võrreldes võib märgata, et neil on erinev intervalliline struktuur (eriti sümboliga X tähistatud kompleksidel). Seetõttu kõlavad nad ka mitmehäälsuses erinevalt.

Näide 1. Harmoonilised kompleksid erinevates helilaadides.

Kahe astmekompleksi reegel seisneb selles, et mitmehäälsuses kõlavad korraga ainult ühe kompleksi astmed. Enamasti kõlavad need kahekaupa, kuid esineb ka kolmehäälseid kooskõlasid. See tähendab, et oma viisivarianti moodustades peab iga leelokoori laulja arvestama sellega, millises rütmis viisis harmoonilised funktsioonid vahelduvad, ja valima harmooniaga sobivad astmed – muidugi teevad seto lauljad seda intuitiivselt, oma harmoonilise rütmi tunnetusest lähtudes. Suurim vastutus lasub seejuures killõ lauljal, kes peab tema kasutuses olevaid väheseid noote vaheldama õiges rütmis, et olla kooskõlas torrõ-partiiga ja anda ka koorile harmooniline orientiir. Selleks peab killõ-lauljal olema eriti hea harmooniatunne, sest tema partii ei ole meloodiliselt reljeefne ja viiside eristamisel ei ole talle abiks kergesti meelde jäävad meloodilised käigud nagu torrõdel.

Näide 2 illustreerib, kuidas on määratud konkreetse viisi harmoonilise rütmi mudel. Harmoonilisi komplekse tähistan sümbolitega X ja O. Pooltoon-poolteisttoon-laadis tähistab sümbol X kompleksi d-fis-ais ja sümbol O kompleksi es-g-h. Neist kompleksidest on viisis kasutatud astmed fis-ais ja g-h. Lõpufunktsiooniks (n-ö „toonikaks“) on selles lauluesituses kompleks X. Harmoonilise rütmi sümbolid on grupeeritud vastavalt viisi meetrumimudelile, mis sõltub omakorda teksti ja viisi rõhurühmadest. Meetrumi- (või rõhu)rühma alustav funktsioon on tähistatud suurtähega. Harmoonilist rütmi olen määranud ainult kooriosas, kuna harmoonilised seaduspärasused avalduvad selgemalt mitmehäälsuses ja kooriosa struktuur on eeslaulja osast märksa stabiilsem.

Näide 2. Viisitüüp I.A.2.a₁; lõpufunktioon X. Moro ääl (pulmalaul), Irina (Ir´o) Liivik kooriga, Meremäe k., 1937 (ERA, Pl. 71 A1).

Huvitav on võrrelda näidet 2 näitega 3, kus sama viisitüüp on esitatud diatoniseeritud kujul – anhemitoonilis-diatoonilises laadis. Selles laadis tähistame sümboliga X tavaliselt astmekompleksi e-a-c ja sümboliga O astmekompleksi e-g-h. Kuigi viisitüübi kahes esituses on häälte meloodialiikumine väga sarnane, osutub anhemitoonilis-diatoonilises laadis lõpufunktsiooniks kompleks O. Kui arvestada, et harmooniliste funktsioonide tähistused on võrreldes näitega 2 vahetuses, on lihtne märgata, et näidetes 2 ja 3 kasutatakse sisuliselt sama HR mudelit.

Näide 3. Viisitüüp I.A.2.a₁; lõpufunktioon O. Pööräjuuskmine (tantsulaul), Eha Kõiv leelokooriga “Kuldatsäuk”, Värska al., 2006 (“Estonie: Chants Seto / Seto Songs”, CD, 2008, nr 11).

Seoses näidetes 2 ja 3 toimunud harmoonilise rütmi tähistuste nihkumisega tuleb märkida, et tegelikult ei ole sümbolid X ja O konkreetsete astmekompleksidega rangelt seotud ega osuta harmooniliste funktsioonide hierarhiale ehk põhifunktsioonile. Sümbolid X ja O olen harmoonilise rütmi tähistamiseks valinud nende graafilise kontrastsuse ja tähendusliku neutraalsuse tõttu. Kui lähtuda näites 1 toodud astmekomplekside tähistustest (need on tüüpilised, kuid võivad konkreetses analüüsis ka vahetusse minna), siis võib pooltoon-poolteisttoon-laadis olla põhifunktsiooniks ehk lõpufunktsiooniks nii O kui ka X. Vanemas diatoonilises laadis on see alati O ja teistes laadides enamasti O, kuigi vahel ka X. Viiside harmoonilist rütmi võrreldes (nagu näidete 2 ja 3 puhul) võib tekkida ka küsimus, kas ei oleks parem tähistada mõnes viisis funktsioone üldise reegliga võrreldes vastupidiselt. Selline probleem tekib tavaliselt seoses heliridade vaheliste üleminekutega (vt Helilaadide segunemine). Näite 3 puhul piisaks astme a madaldamisest as-iks (bemolli lisamisest võtmesse), et anhemitoonilis-diatooniline laad muutuks (taas) pooltoon-poolteisttoon-laadiks (e-g-as-h-c = es-fis-g-ais-h; struktuur 3-1-3-1) – sel juhul oleksid HR mudeli tähistused 2. ja 3. näites ühesugused. Samas ei pruugi vastupidine funktsioonide tähistamine olla hea lahendus siis, kui võrdlusesse lisada veel kolmas viis mõnes teises laadis.

Valisin harmoonilise rütmi viisitüübi peamiseks representatiivseks tunnuseks mitte ainult selle stabiilsuse tõttu, vaid ka seetõttu, et see aitab eristada viisitüüpe isegi siis, kui nende muud struktuursed tunnused langevad kokku. Heaks näiteks on viisitüübid I.A.2.a₁ ja I.A.2.a₂ (esimene neist on toodud näidetes 2 ja 3 ning teine näidetes 4, 5 ja 6).

Näide 4. Viisitüüp I.A.2.a₂; pooltoon-poolteisttoon-laad. Juri Gagarinile (improvisatsioon), Agripina (Kreepa) Pihlaste kooriga, Haudjasaare k., 1961 (EKRK, Fon. 23 (12)).

Mõlemas viisitüübis on tegemist sama meetrumimudeliga 3 + 2 + 2 + 2 + 2 ja peaaegu sama silbirütmi mudeliga /      (erinevus on ainult ühes mittekohustuslikus silbijaotuses). Ka värsirea struktuur on mõlemal viisitüübil peaaegu sama – aabcd ja aabcd. Erinevad aga HR mudelid: Oxo Xx ’ Xx Oo Xx ja Xox ’ Ox Oo ’ Ox Oo. HR erinevuste tõttu on viisiridade tsesuurid eri kohtades (vt ülakomasid HR skeemides). Vaadeldavate viisipüüpide puhul väärib tähelepanu see, et pooltoon-poolteisttoon-laadis viisid lõpevad erineva harmoonilise funktsiooniga – astmekompleksiga X viisitüübis I.A.2.a₁ ja kompleksiga O viisitüübis I.A.2.a₂. Viiside põhifunktsiooni erinevus on oluline, sest siin me ei võrdle erinevates helilaadides esitusi (nagu näidete 2 ja 3 puhul), vaid kahte pooltoon-poolteisttoon-laadis esitust (näited 2 ja 4). Näites 2 lõpeb viis kooskõlaga fis-ais (funktsioon X) ja näites 4 on lõpukooskõlaks es-g (funktsioon O), mis on nende kahe viisitüübi tähtis eristav tunnus.

Viisitüüpi I.A.2.a₂ esitatakse samuti diatoonilises laadis (näide 5), kuid sel juhul ei kaasne helirea muutusega erinevust harmoonilise rütmi tähistuses, nagu see oli viisitüübi I.A.2.a₁ kahe variandi puhul (näited 2 ja 3). Näites 5 leiame samasuguse HR mudeli nagu näites 4 – Xox ’ Ox Oo ’ Ox Oo.

Näide 5. Viisitüüp I.A.2.a₂; uuem diatooniline laad. Kui ma inne kar´ah käve (lüürika), Anne Pähnapuu kooriga, Põrste k., 1973 (RKM, Mgn. II 2421 b).

Mõne viisitüübi puhul esineb selline huvitav nähtus nagu harmoonilise rütmi inversioon. See tähendab, et viisitüübi erinevad esitused järgivad HR mudelit peegelpildis, kusjuures tegemist ei ole pelgalt funktsioonide tähistamise probleemiga (nagu näidetes 2 ja 3). Tõelise inversiooni näide leidub viisitüübis I.A.2.b₁, rahvapärase nimega pöörä ääl. See on väga levinud viisitüüp, kus kasutatakse erinevaid heliridu ning harmoonilise rütmi variante, kuid mis on sellest hoolimata kergesti äratuntav. Näidetes 6 ja 7 saab võrrelda pöörä ääle kahte pooltoon-poolteisttoon-laadis esitust. Esimesel juhul on viisi HR mudeliks Xo Xx Ooo ’ Xo Xx Oo; teisel juhul on see Ox Xo Xox ’ Ox Xo Xx. Need esitused suhestuvad omavahel kui variatiivsed inversioonid.

Näide 6. Viisitüüp I.A.2.b₁; lõpufunktsioon O. Kalmuneiu (lüroeepika), Elena (Oll´o) Laanetu kooriga, Suure-Rõsna k., 1972 (RKM, Mgn. ER 55 (1)).

Näide 7. Viisitüüp I.A.2.b₁; lõpufunktsioon X.  Püürä_ks, püürä (pööräjuuskmine), Anne Vabarna kooriga, Tonja k., 1936 (ERA, Pl. 23 A2).

Kuna nende kahe esituse HR ei ole mitte ainult inversioonis, vaid ka varieerub mõnevõrra, siis muutub inversiooni printsiip paremini nähtavaks, kui võrrelda harmoonilist rütmi üldistatud kujul. Näites 6 on harmoonilise rütmi üldistatud mudeliks X–x O-o, näites 7 on see aga vastupidine O–o X-x (harmoonilise rütmi üldistamisest tuleb juttu allpool).

Inversioonide puhul tekib küsimus, kas selline erinevus on piisav, et käsitleda esitusi eraldi viisitüüpidena, või tuleks neid vaadelda sama viisitüübi erinevate versioonidena. Olen teinud tüpoloogias mõlemat moodi, sõltuvalt sellest, kas harmoonilise rütmi inversiooniga kaasnesid ka muud stabiilsed erinevused.

Veel üks teema, millel tuleks peatuda, on üldistatud harmooniline rütm. Nii silbirütmi kui ka harmoonilise rütmi modelleerimisel tekib mõnikord vajadus taandada väiksema struktuurse kaaluga elemente, et esile tuua üldisem mudel. Näiteks kasutasin eespool harmoonilise rütmi üldistamist, et võrrelda harmoonilise rütmi inversiooniga viisivariante (näited 6 ja 7). Kui viisitüübis esineb nii järgnevust Oxo kui ka Ooo, siis on ilmne, et funktsioon X on siin n-ö „kõrvalakord“ (“abiakord”) ning järgnevuse üldiseks sisuks on funktsiooni O „prolongeerimine“ (O-o). Sama põhimõtte järgi taandasin pöörä ääles variandid Xo Ox, Xo Xx ja Xx Xx üldiseks skeemiks X–x. Harmoonilise rütmi üldistamine muutub eriti tähtsaks analüüsivõtteks II rütmisüsteemi viisides, mis on pikemad ja kus on rohkem silbijaotusi. Seda illustreerivad näited viisitüübist II.C.3.a (näited 8 ja 9).

Näide 8. Viisitüüp II.C.3.a. Jaanilaul (kalendritavandi laul), Elena (Oll´o) Laanetu kooriga, Suure-Rõsna k., 1976 (Jaan Sarve salvestus ER stuudios; Estonie: Chants Seto, CD 2008, nr 6).

Näide 9. Lää ma alla hainale (töölaul), Tepo Nabra kooriga, Krantsova k., 1913 (ERA, Fon. 100 c).

Kahe esituse HR mudel erineb neljas positsioonis (need on allpool skeemides esile toodud paksus kirjas), kuid kõigil juhtudel on tegemist „abiakordidega“, millel on vähe struktuurset kaalu. Kuna viisitüübi meetrumiühikuks on veerandnoot, siis oleks loogiline üldistada harmoonilist rütmi veerandnootide tasandini. Kui see on tehtud, tuleb välja lihtne mudel OO ‘ XXXX ‘ OOXX. Mudel on mõlemal viisivariandil sama, näidates nende omavahelist sugulust:

Ooxo ‘ Xx Xx Xxxx ‘ Ooxo Xxxx

Oooo ‘ Xo Xx Xxox ‘ Oooo Xxxx

Üldistatud (veerandnootides):

OO ‘ XXXX ‘ OOXX

Viisi harmoonilist rütmi on võimalik veelgi üldistada, sest veerandnoodid grupeeruvad siin kahekaupa. Poolnootides oleks viisitüübi HR mudel OXX’OX. Harmoonilise rütmi kõige üldisem tasand, mis on juba väljaspool rütmi, näitab viisi harmoonilist üldprintsiipi – funktsiooni O üleminekut funktsiooni X, mis toimub kaks korda viisirea vältel: O→X ’ O→X.

Harmoonilise rütmi mitmetasandiline üldistamine aitab paremini kirjeldada pikema viisireaga viise ja näitab harmooniliste järgnevuste üldisemat loogikat. Siin tüpoloogias piirdun siiski valdavalt üldistamisega veerandnoodi tasandini, sest viisitüübi määramiseks sellest piisab.